Search Algorithms

Search algorithm --- method for finding an item or group of items with specific properties within a collection of items.
Collection could be implicit
- example --- find square root as a search problem
  - Exhaustive enumeration
  - Bisection search
  - Newton-Raphson method
- Collection could be explicit
  - Example --- is a student record in a stored collection of data?

Searching algorithms:

Linear search
- Brute force search (aka Museum algorithm)
- List does not have to be sorted
- Search for an element is O(n)
Binary search
- List must be sorted to give correct answer
- Saw two different implementations of this algorithm: with and without copying
- Search for an element is O(log n) (for the implementation that avoids copying)
When does it make sense to sort first then search (using binary search)?
- SORT + O(log n) < O(n), or SORT <O(n)-O(log n)
- When is SORT less than O(n)? NEVER! To sort a collection of n elements, you must look at each element at least once!

Amortized cost

Why may one bother sorting first?

In some cases, may sort the list once, and then do many searches
Amortize cost of the sort over many (say K) searches
SORT + k*O(log n) < K*O(n)
- For large K, SORT time becomes irrelevant, if cost of sorting is small enough

Sort Algorithms

Want to efficiently sort a list of entries
Will see a range of methods, including one that is quite efficient

Monkey sort

Also known as bogosort, stupid sort, slow sort, permutation sort, shotgun sort
To sort a deck of cards:
1. Throw them in the air
2. Pick them up
3. Are they sorted?
4. Repeat if not sorted

def bogo_sort(L):
  while not is_sorted(L):
    random.shuffle(L)

best case: O(n) where n is len(L) to check if sorted
worst case: O(?) it is unbounded if really unlucky

Bubble sort

Compare consecutive pairs of elements
Swap elements in pair such that smaller is first
When reach end of list, start over again
Stop when no more swaps have been made
Largest unsorted element always at end after pass, so at most n passes

In this animation, we assume that the first n integers are present in the list in a random order. As the passes of bubble sort proceed, the largest elements start identifying their correct position, e.g., the integer of value n is at the nth index.

Code:

def bubble_sort(L):
  swap = False
  while not swap:  # O(len(L))
    swap = True
    for j in range(1, len(L)):  # O(len(L))
      if L[j-1] > L[j]:
        swap = False
        temp = L[j]
        L[j] = L[j-1]
        L[j-1] = temp

Inner loop is for doing the comparisons
Outer while loop is for doing multiple passes until no more swaps
O(n²) where n=len(L) to do n-1 comparisons and n-1 passes.

Selection sort

First step
- Extract minimum element
- Swap it with element at index 0
Subsequent step
- In remaining sublist, extract minimum element
- Swap it with the element in index 1
Keep the left portion of the list sorted
- At ith step, first i elements in the list are sorted
- All other elements are bigger than the first i elements

Analyzing slection sort

Loop invariant
- Given prefix of list L[0:i] and suffix L[i:len(L)], then prefix is sorted and no element in prefix is larger than the smallest element in the suffix.
  1. Base case: prefix empty, suffix whole list -- invariant true
  2. Induction step: move minimum element from suffix to the end of prefix. Since invariant true before move, prefix sorted after append. Also, no element in prefix larger than the smallest element in the suffix still holds.
  3. When exit, prefix is entire list, suffix empty, so list sorted.

Complexity of selection sort

def selection_sort(L):
  suffixSt = 0
  while suffixSt != len(L):     # executed len(L) times
    for i in range(suffixSt, len(L)):   #executed len(L) - suffixSt times
      if L[i] < L[suffixSt]:
        L[suffixSt], L[i] = L[i], L[suffixSt]
    suffixSt += 1

Outer loop executes len(L) times
Inner loop executes len(L)-suffixSt times
Complexity of selection sort is (where n=len(L)): n+(n-1)+(n-2)+...+(n-n) or O(n²).

Merge sort

Use a divide-and-conquer approach:

If list is of length 0 or 1, already sorted
If list has more than one element, split into two lists and sort each
- Sorting of smaller lists is self-similar
Merge sorted sublists
1. Look at the first element of each, move smaller to end of the result
2. When one list empty, just copy rest of other list

Idea:

Divide and conquer
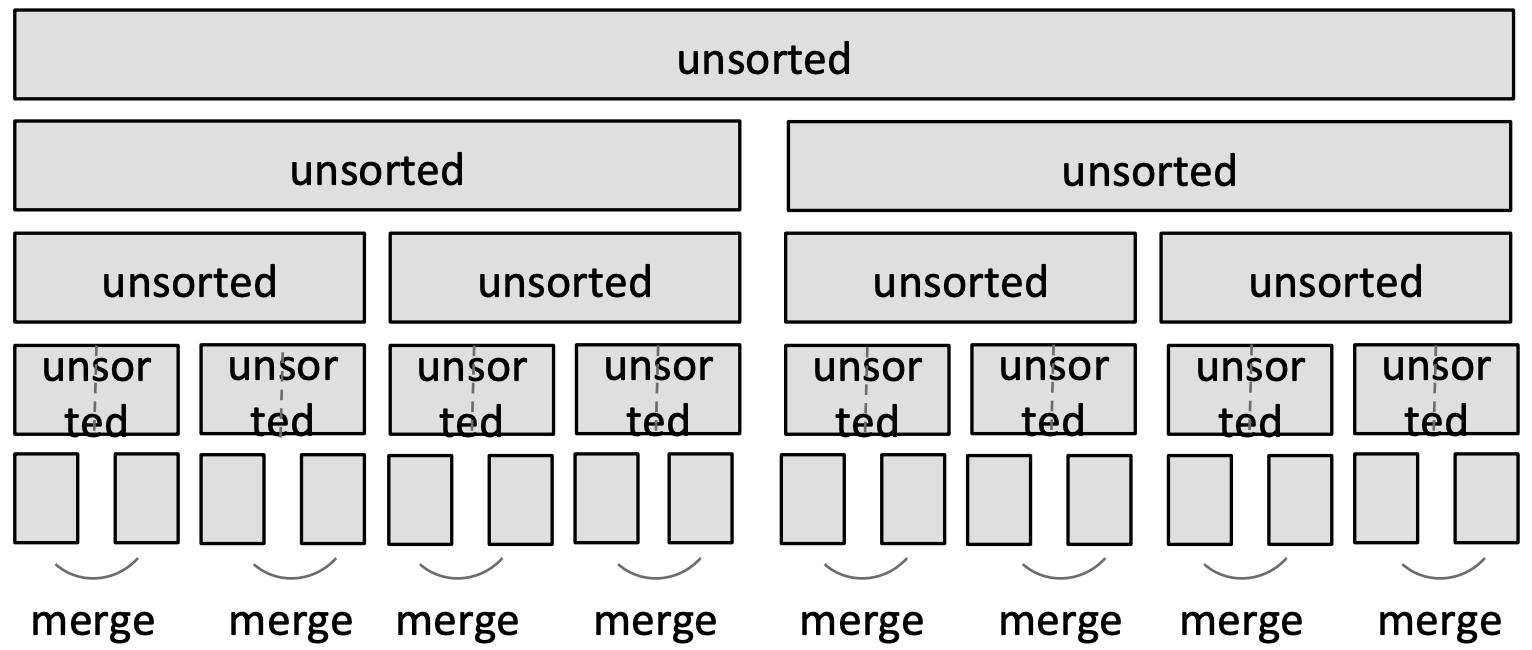
Split list in half until have sublists of only one element.
Merge such that sublists will be sorted after merge
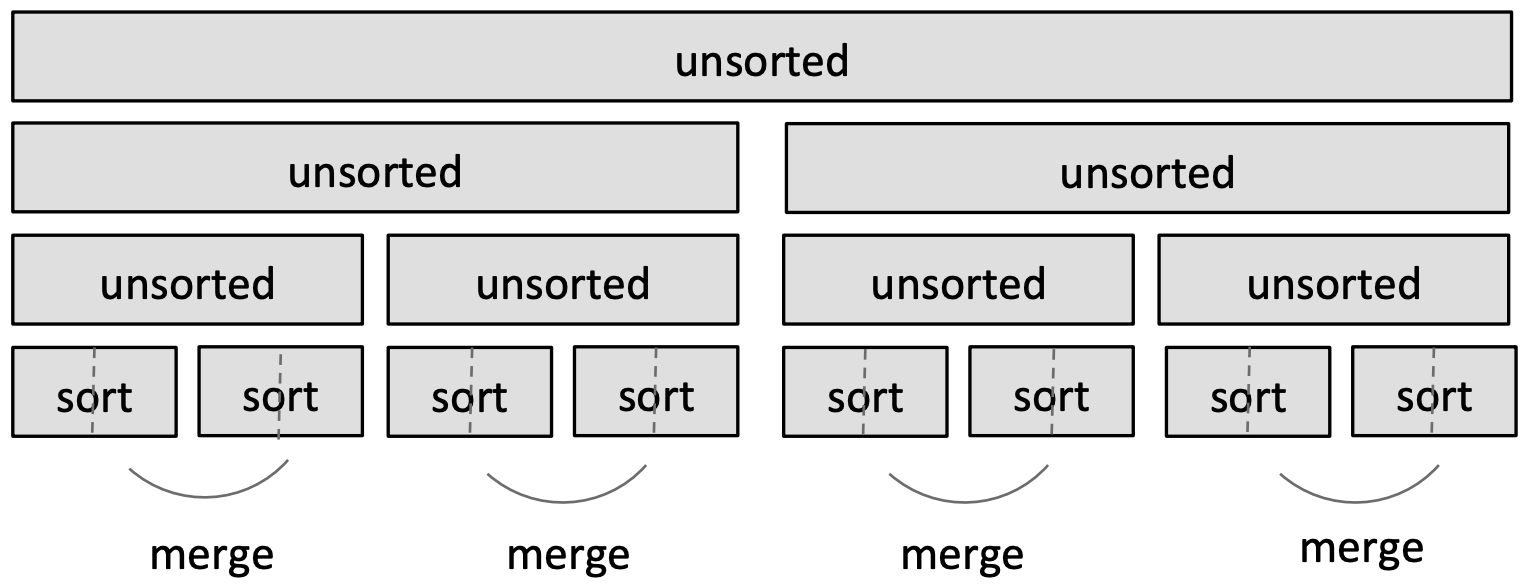
Merge sorted sublists; sublists will be sorted after merge.
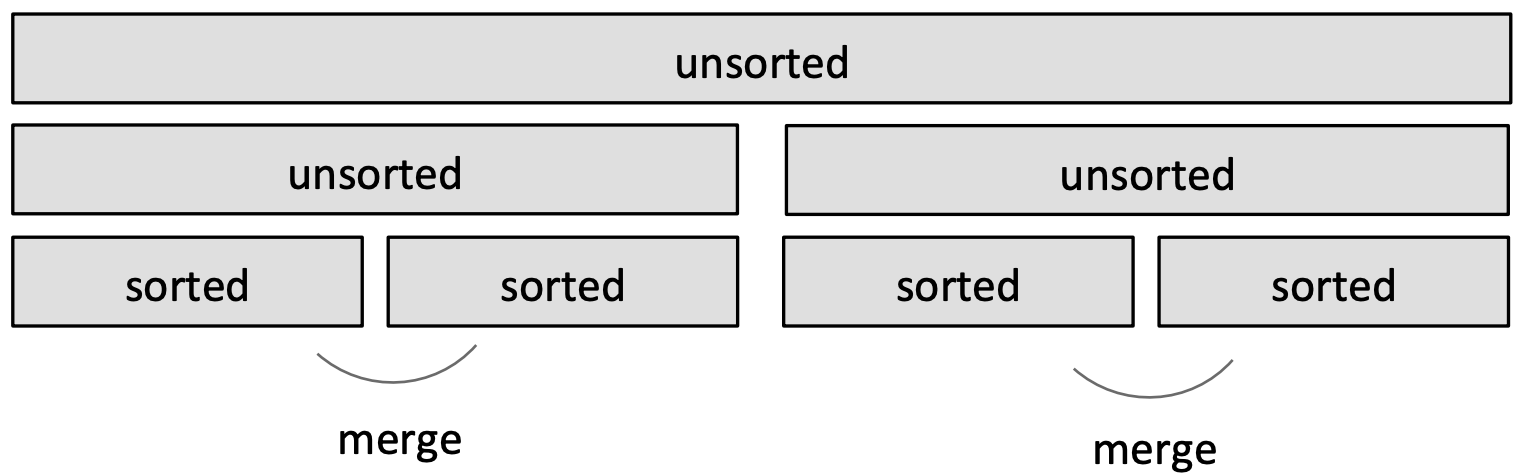
Again.
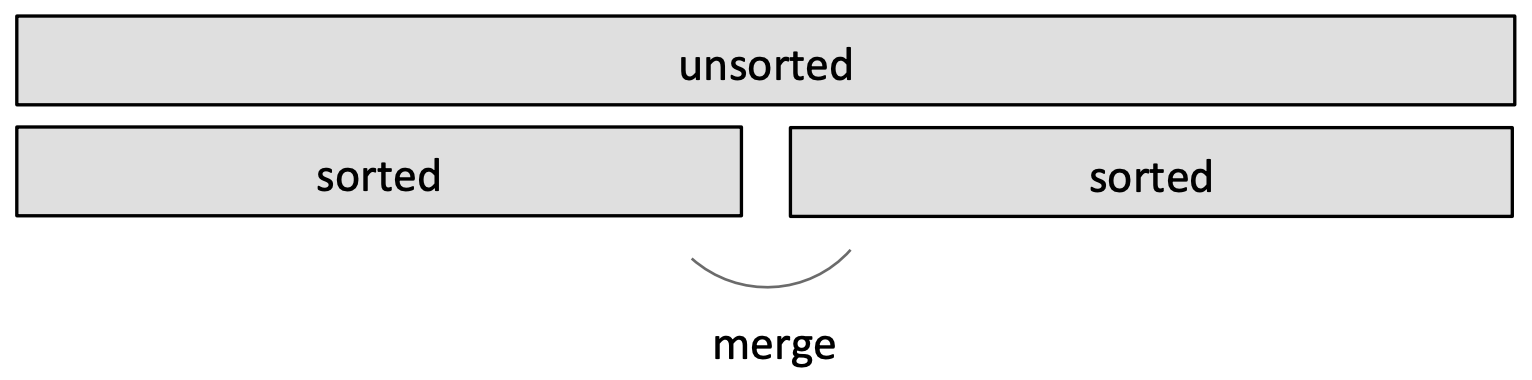
Done!

Example of merging:

Left in list 1 Left in list 2 Compare Result

[1,5,12,18,19,20] [2,3,4,17] 1, 2 []

[5,12,18,19,20] [2,3,4,17] 5, 2 [1]

[5,12,18,19,20] [3,4,17] 5,3 [1,2]

[5,12,18,19,20] [4,17] 5,4 [1,2,3]

[5,12,18,19,20] [17] 5,17 [1,2,3,4]

[12,18,19,20] [17] 12,17 [1,2,3,4,5]

[18,19,20] [17] 18,17 [1,2,3,4,5,12]

[18,19,20] [] 18,-- [1,2,3,4,5,12,17]

[] [] 18,-- [1,2,3,4,5,12,17,18,19,20]

Merging sublists step

def merge(left, right):
  result = []
  i, j = 0, 0
  while i < len(left) and j < len(right):
    #left and right sublists are ordered.
    #move indices for sublists depending on which sublist holds next smallest element
    if left[i] < right[i]:
      result.append(left[i])
      i += 1
    else:
      result.append(right[j])
      j += 1
  while i < len(left):
    #when right sublist is empty
    result.append(left[i])
    i += 1
  while j < len(right):
    #when left sublist is empty
    result.append(right[j])
    j += 1
  return result

Complexity of merging sublists step

Go through two lists, only one pass
Compare only smallest elements in each sublist
O(len(left)+len(right)) copied elements
O(len(longer list)) comparisons
Linear in length of the lists

Mergesort algorithm recursive

def merge_sort(L):
  if len(L) < 2:
    return L[:]   #base case
  else:
    middle = len(L)//2
    left = merge_sort(L[:middle])  #divide; first half
    right = merge_sort(L[middle:]) #divide; second half
    return merge(left, right)

Divide list successively into halves.
Depth-first such that conquer smallest pieces down one branch first before moving to larger pieces.
Notice that we are copying the lists while seeting up the recursive calls, and also inside merge(). We do not worry about it because the merge() step is anyway O(n).

Complexity of mergesort

At first recursion level
- n/2 elements in each list, where n is len(L)
- c1*n/2 [copy] + c1*n/2 [copy] + c2*n [merge] = (c1+c2)*n
At second recursion level
- n/4 elements in each list
- Two merges: 2*(c1*n/4 [copy] + c1*n/4 [copy] + c2*n/2 [merge]) = (c1+c2)*n
At kth recursion level
- n/2^k elements in each list
- 2^k merges: 2^k*(c1*n/2^k+1 [copy] + c1*n/2^k+1 [copy] + c2*n/2^k [merge]) = (c1+c2)*n
Each recursion level is O(n)
Number of recursion levels is O(log n)
Overall complexity: O(nlog n)

Sorting summary:

Bogo sort
- randomness, unbounded O()
Bubble sort
- O(n²)
Selection sort
- O(n²)
Mergesort
- O(n log n)
Claim (without proof): O(n log n) is the fastest sort there can be for elements of arbitrary type.

Left in list 1	Left in list 2	Compare	Result
[1,5,12,18,19,20]	[2,3,4,17]	1, 2	[]
[5,12,18,19,20]	[2,3,4,17]	5, 2	[1]
[5,12,18,19,20]	[3,4,17]	5,3	[1,2]
[5,12,18,19,20]	[4,17]	5,4	[1,2,3]
[5,12,18,19,20]	[17]	5,17	[1,2,3,4]
[12,18,19,20]	[17]	12,17	[1,2,3,4,5]
[18,19,20]	[17]	18,17	[1,2,3,4,5,12]
[18,19,20]	[]	18,--	[1,2,3,4,5,12,17]
[]	[]	18,--	[1,2,3,4,5,12,17,18,19,20]