Recap

Why do we want to understand the efficiency of programs?

How can we reason about an algorithm in order to predict the amount of time it will need to solve a problem of a particular size?
How can we relate choices in algorithm design to the time efficiency of the resulting algorithm?
- Are there fundamental limits on the amount of time we will need to solve a particular problem?

Goals:

Want to evaluate program's efficiency when input is very big
Want to express the growth of program's runtime as input size grows
Want to put an upper bound on growth --- as tight as possible
Do not need to be precise: order of not exact growth
We will look at the largest factors in runtime
- Which section of the program will take the longest to run?
Thus, generally we want a tight upper bound on growth as function of size of input, in worst case

Complexity classes in increasing order:

O(1) denotes constant running time
O(log n) denotes logarithmic running time
O(n) denotes linear running time
O(n log n) denotes log-linear running time
O(n^c) denotes polynomial running time (c is a constant)
O(cⁿ) denotes exponential running time (c is a constant being raised to a power based on size of input)

Class	n=10	n=100	n=1000	n=1000000
O(1)	1	1	1	1
O(log n)	1	2	3	6
O(n)	10	100	1000	1000000
O(n log(n))	10	200	3000	6000000
O(n^2)	100	10000	1000000	1000000000000
O(2^n)	1024	1.2*10^31	1.07*10^311	forget it!

Complexity classes in more detail

Constant complexity class

Complexity independent of input
Very few interesting algorithms in this complexity class, but can often have pieces that fit this class
Can have loops or recursive calls, but ONLY IF number of iterations or calls independent of input size

Logarithmic complexity class

Complexity grows as log of size of one of the inputs
Examples: bisection search

Searching in a list

Suppose we want to know if a particular element is present in a list
Suppose we know that the list is ordered from smallest to largest

Saw previously that we could just "walk down" the list, checking each element

def search(L, e):
  for i in range(len(L)):
    if L[i] == e:
      return True
    if L[i] > e:
      return False
  return False

This method is called a sequential search.

Sequential search complexity is linear in length of the list. Can we do better?

Recursive Big-O

Below is the "pseudocode" for finding BigO of a non-recursive function. Note that this is not real code; this is to show the recursive nature of BigO

Self-similarity: find BigO of smaller code blocks and combine them The BigO pseudocode does not cover function calls and some other cases (to keep the discussion simple) --- though experiment to expand this

findBigO(codeSnippet):
  if codeSnippet is a single statement:
    return O(1)
  if codeSnippet is a loop:
    return number_of_times_loop_runs * findBigO(loop_inside)
  for codeBlock in codeSnippet:
    return the_sum_of findBigO(codeBlock)

What are the subproblems? loop_inside and codeBlock.
How are the results of subproblems combined? Using "number_of_times_loop_runs" and "the_sum_of"
Where are the recursive calls? calls to findBigO(loop_inside) and findBigO(codeBlock)
What is the base case? single statement
Are we following the 3 rules of recursion? e.g., are we moving towards the base case in the recursive call?
Example: compute bigO for the following code using this recursive pseudocode:
```
for i in range(N * N):
  for j in range(3, 219):
    print("sum: ", i + j)
print("Enjoy COL100");
```
Show the working of findBigO on this code snippet.

Binary search

Interested in search for element e in list L
Pick an index i that divides list in half
Ask if L[i] == e
If not, ask if L[i] is larger or smaller than e
Depending on answer, search left or right half of L for e.

Self-similarity: the same search can be executed on a smaller list (of around half size)
Base-cases: when list is empty or a single element

Answer to smaller problem is the answer to the original problem

Binary search complexity analysis

Let the original size of the list be n.
In the ith steps, the size of the list is n/2ⁱ.
Will finish looking through the list when 1 = n/2ⁱ, and so i (the number of total steps) is log n.
Complexity of recursion is O(log n) where n is len(L).

Binary search implementation 1

def binsearch1(L, e):
  if L == []:             # this check and return is constant-time-complexity, or O(1)
    return False    
  elif len(L) == 1:       # this check is also O(1)
    return L[0] == e      # this check is also O(1)
  else:
    half = len(L)//2      # constant O(1)
    if L[half] > e:    # Is L[half] O(1)?  Let's assume for now it is.
      return binsearch1(L[:half], e)   # involves copying the list, not constant
    else:
      return binsearch1(L[half:], e)   # involves copying the list, not constant

Complexity of binsearch1:

O(log n) calls to binsearch1
- On each recursive call, size of range to be searched is cut in half.
- If original range is of size n, in worst case in case of range of size 1 when n/2^k=1, or k=log n
- O(n) for each binsearch1 call to copy list:
  - This is the cost to set up each call (as a call involves creating a new list by copying elements from the incoming list), so do this for every level of recursion.
- O(log n)*O(n) indicates that the complexity can be as high as O(n log n).
- A more careful analysis: in the ith recursive call, the cost of setting up the call is O(n/2ⁱ). Thus, the total cost of copying is n + n/2 + n/2² + ... + 1, which is equal to 2n.

A better implementation of binary search

Still reduce the size of problem by a factor of two on each step
But just keep track of low and high portion of list to be searched
- Will need a helper function to keep track of these additional parameters
Avoid copying the list
The complexity of recursion is again O(log n) where n=len(L).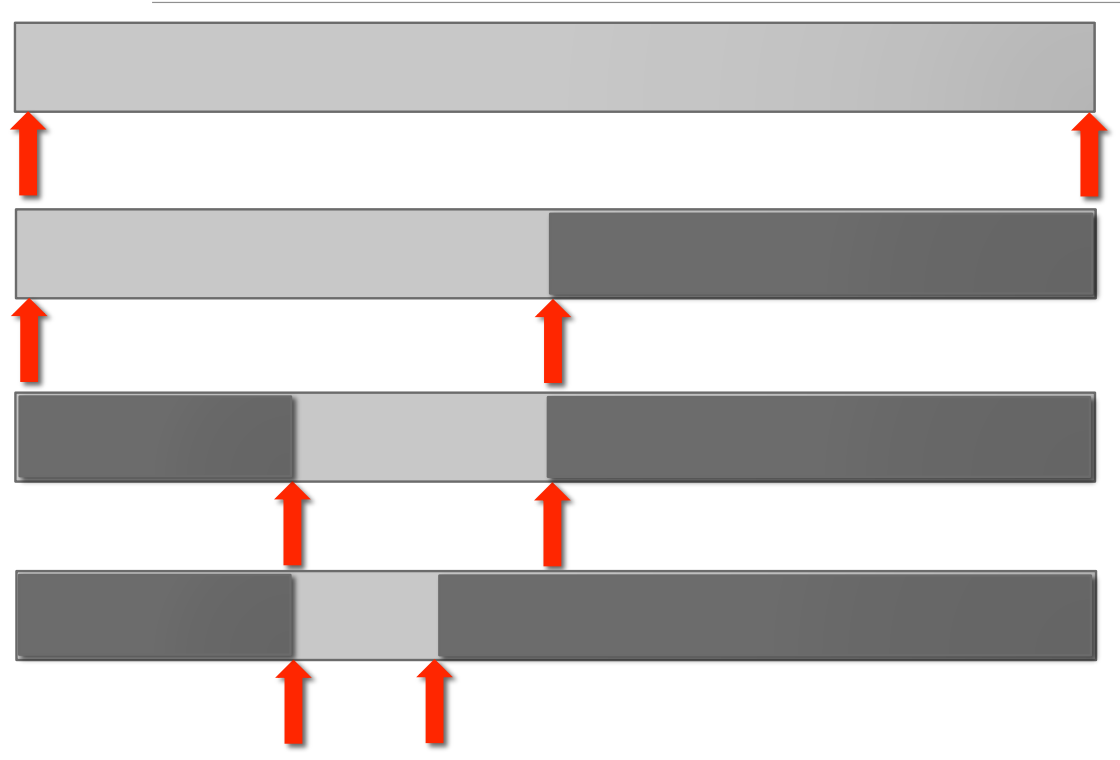

def binsearch_helper(L, e, low, high):
  if high == low:
    return L[low] == e
  mid = (low + high)//2
  if L[mid] == e:
    return True
  elif L[mid] > e:
    if low == mid:   #nothing left to search
      return False
    else:
      return binsearch_helper(L, e, low, mid - 1)    #constant to set up the call.  The actual call takes longer
  else:
    return binsearch_helper(L, e, mid + 1, high)  #constant to set up the call.  The actual call takes longer

def binsearch(L, e):
  if len(L) == 0:
    return False
  else:
    return binsearch_helper(L, e, 0, len(L) - 1)  #constant to set up the call.  The actual call takes longer

Complexity of binsearch:

O(log n) calls to binsearch_helper
On each recursive call, size of range to be searched is cut in half.
If original range is of size n, in worst case in case of range of size 1 when n/2^k=1, or k=log n
O(1) for each binsearch_helper execution (including the cost to set up the call)
O(log n)*O(1) indicates that the complexity is O(log n).

Another example of logarithmic complexity: int2str

def int2str(n):
  digits = '0123456789'
  if n == 0:
    return '0'
  result = ''
  i = n
  while i > 0:
    result = digits[i%10] + result
    i = i//10
    # can you place an assertion here?
  return result

What is the correctness argument? What assertion can you put at the end of the body of the while loop? Ans: assert(10**(len(result))*i+int(result)==n). This is an invariant.

Analyzing the complexity of the program above:

Only have to look at loop as no function calls
Within while loop, execute a constant number of steps
How many loop iterations do we execute?
- How many times can we divide n by 10 such that it remains greater than 0?
- O(log(n))
What is the cost of each loop iteration?
- Integer division is O(1)
- Construction of result is O(len(result)) as it involves a copy, which is O(log n) in the worst case and average case.
- Thus the cost of a loop iteration is O(log n).
Total cost: O(log² n).

How can you change the implementation so it takes O(log n) time?

Let result be a list, initialized to [] and appended-to using the append() function (which is O(1))
At the end of the loop, reverse the list (O(len(result))) and join it to form a string (again O(len(result))).

Linear complexity

Sequential search in a list to check the presence of an element
Iterative loops

Analyzing the complexity of an iterative implementation of the factorial function

Complexity can depend on the number of iterative calls

def fact_iter(n):
  prod = 1
  for i in range(1, n+1):
    prod *= i
  return prod

Overall, O(n). n times around loop, constant time each time.

Analyzing the complexity of a recursive implementation of the factorial function

def fact_rec(n):
  """ assume n >= 0 """
  if n <= 0:
    return 1
  else:
    return n*fact_rec(n-1)

Computes factorial recursively
If you time it, you may notice that it runs a bit slower than iterative versions due to function calls
Still O(n) because the number of function calls is linear in n, and constant effort to set up call.
For factorial, iterative and recursive implementations are the same order of growth.

Log-linear O(n log n) complexity

Many practical algorithms are log-linear
Very commonly used log-linear algorithm is merge-sort
Will return to this in the next lecture

Polynomial complexity

Most common polynomial algorithms are quadratic, i.e., complexity grows with the square of size of input
This commonly occurs when we have nested loops or recursive function calls

Saw this previously in the isSubset function:

def isSubset(L1, L2):
  for e1 in L1:
    matched = False
    for e2 in L2:
      if e1 == e2:
        matched = True
        break
    if not matched:
      return False
  return True

Exponential complexity

Recursive functions where more than one recursive call for each size of problem
- Towers of Hanoi
Many important problems are inherently exponential
- Unfortunate as cost can be high
- Will lead us to consider approximate solutions as may provide reasonable answer more quickly
- Examples: knapsack problem, N-queens problem, ...

Complexity of Towers of Hanoi

Let t_n denote time to solve tower of size n.
t_n = 2t_n-1 + 1 = 2(2t_n-2 + 1) + 1 = 4t_n-2+ 2 + 1
4t_n-2+ 2 + 1 = 4(2t_n-3+1)+2 + 1 = 8t_n-3 + 4 + 2 + 1
After k expansions: 2^kt_n-k+2^k-1 + 2^k-2 + ... + 4 + 2 + 1
When n-k=1: 2^n-1 + 2^n-2 + 2^n-3 + ... + 4 + 2 + 1
Which is equal to: 2ⁿ-1.
So order of growth is 2ⁿ.

Exponential complexity example: Power set

Given a set of integers (with no repeats), want to generate a collection of all possible subsets, called the power set.

{1, 2, 3, 4} would generate (order does not matter):

{}, {1}, {2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {3}, {4}, {1,2}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}

Power set --- concept

We want to generate the power set of integers from 1 to n
Assume we can generate power set of integers from 1 to n-1
Then all of those subsets belong to bigger power set (choosing not include n); and all of those subsets with n added to each of them belong to the bigger power set.
nice recursive description!

Exponential complexity

def genSubsets(L):
  res = []
  if len(L) == 0:
    return [[]]  # list of empty list
  smaller = genSubsets(L[:-1]) #all elements without last element
  extra = L[-1:]
  new = []
  for small in smaller:
    new.append(small+extra)  # for all smaller solutions, add one with last element
  return smaller+new  # combine those with last element and those without

Assumptions:

append() is constant time
However, small+extra can be O(n) time.

Method:

Time includes time to solve smaller problem, plus time needed to make a copy of all the elements in the smaller problem.
Important to think about size of the solution of the smaller problem
We already know that for a set of size k, the solution is of size 2^k.
How can we deduce the overall complexity from all this information?

Let's analyze:

Let t_n denote time to solve problem of size n.
Let s_n denote size of solution to a problem of size n.
t_n=t_n-1+c3*n*s_n-1+c1*s_n-1+c2 (where c1,c2,c3 are some constants)
t_n>=t_n-1+c1*2^n-1+c2
>=t_n-2+c1*2^n-2+c1*2^n-1+2*c2
>=t_n-k+c1*2^n-k+c1*2^n-k-1+...+2^n-1+k*c2
>=t₀+c1*2⁰+c1*2¹+...+c1*2^n-1+n*c2
>=1+c1*2ⁿ+n*c2
>O(2ⁿ)

Summary of examples of complexity classes

O(1): code does not depend on size of the input
O(log n): reduce problem in half with constant effort at each step
O(n): simple iterative or recursive programs with a single loop or linear recursion
O(nlog n): will see next time
O(n^c): nested loops or recursive calls
O(cⁿ): multiple recursive calls at each level, where the number of levels is linear in n

Example: Iterative Fibonacci

def fib_iter(n):
  if n == 0:    # O(1)
    return 0    # O(1)
  elif n == 1:  # O(1)
    return 1    # O(1)
  else:         # O(1)
    fib_i = 0   # O(1)
    fib_ii = 1  # O(1)
    for i in range(n-1):      # the loop executes O(n) iterations
      tmp = fib_i             # O(1)
      fib_i = fib_ii          # O(1)
      fib_ii = tmp + fib_ii   # O(1)
    return fib_ii             # O(1)

Analysis:

Best case: O(1)
Worst case: c1*O(1) + O(n)*c2*O(1) = O(n)

Example: Recursive Fibonacci

def fib_rec(n):
  """ assumes n an int >= 0 """
  if n == 0:    # O(1)
    return 0    # O(1)
  elif n == 1:  # O(1)
    return 1    # O(1)
  else:         # O(1)
    return fib_rec(n-1) + fib_rec(n-2)

Draw tree. Show the growth for small values of n. Claim (without proof) that the complexity is exponential, slightly lower than 2ⁿ.

Big-O summary

compare efficiency of algorithms
- notation that describes growth
- lower order of growth is better
- independent of machine or specific implementation
Use big-O:
- describe order of growth
- asymptotic notation
- upper bound
- worst case analysis

Complexity of common Python functions

Lists: n is len(L)

index: O(1)
store: O(1)
length: O(1)
append: O(1)
== : O(n)
remove: O(n)
copy: O(n)
reverse: O(n)
iteration: O(n)
in list: O(n)

Dictionaries: n is len(d)

worst case
- index: O(n)
- store: O(n)
- length: O(n)
- delete: O(n)
- iteration: O(n)
average case
- index: O(1)
- store: O(1)
- delete: O(1)
- iteration: O(n)