Understanding Program Efficiency

• A modern computer can execute over a billion instructions per second. So maybe program efficiency does not matter?
  • Some algorithms grow exponentially, e.g., finding prime numbers, compiler optimization algorithms
  • Need to tackle trillions of bytes of data, e.g., search engine
  • Some algorithms require both data and computation, e.g., large-language models
• There are multiple possible programs that achieve the same objective. How can we decide which program is most efficient?

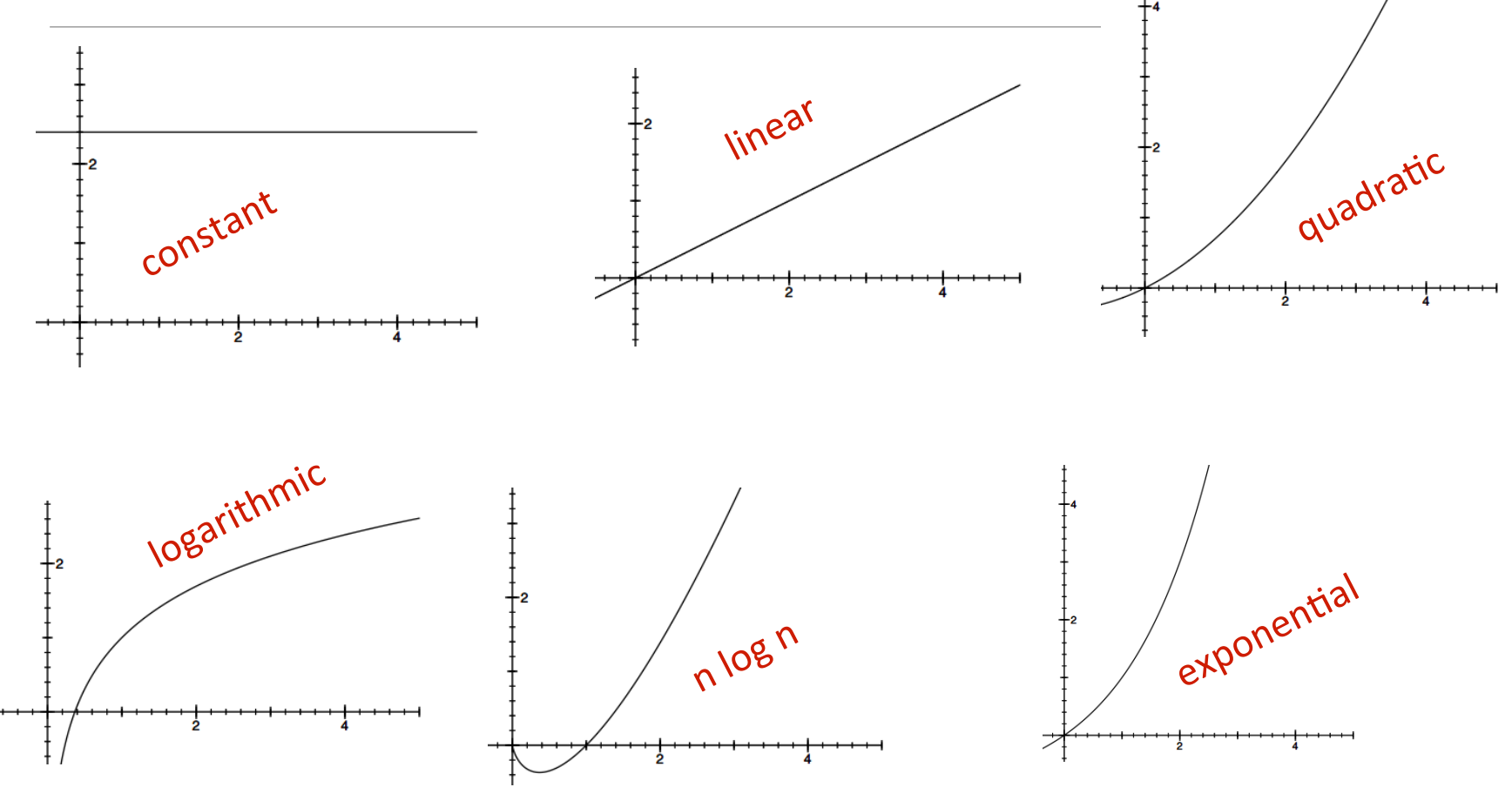
Time vs. Space Efficiency

• Sometimes more space efficient algorithms are also more time efficient, e.g., fib-iterative is more space- and time-efficient than fib-recursive.
• Sometimes, there is a tradeoff between space and time efficiency
  • Can create copies of inputs, or use large data structures for efficient lookup for an overall faster algorithm
• Can store 1000s of Gigabytes (trillions of bytes) in a modern computer's memory and disk
• Will focus on time efficiency

Want to understand efficiency of programs. But there are challenges in understanding efficiency of solution to a computational problem:

• A program can be implemented in many different ways
• You can solve a problem using only a handful of different algorithms
• Would like to separate choices of implementation from choices of more abstract algorithm

How to evaluate efficiency of programs

• Measure with a timer
• Count the operations
• Abstract notion of order of growth
  • Will argue that this is the most appropriate ways of assessing the impact of choices of algorithm in solving a problem; and measuring the inherent difficulty in solving a problem

Timing a program

• use time module: import time
  • recall that importing means to bring in that class into your own file
• Use the clock function to record the current physical time

  import time
  def c2f(c):
    return c*9/5 + 32
  
  t0 = time.perf_counter()
  c2f(100000)
  t1 = time.perf_counter() - t0
  print("call took", t1, "s")
  

time.perf_counter_ns()

Timing programs is inconsistent

• Goal: to evaluate different algorithms
• running time varies between algorithms. Good
• running time varies between implementations. Bad
• running time varies between computers. Bad
• running time is not predictable based on small inputs. Bad
• time varies for different inputs but cannot really express a relationship between inputs and time. Bad

Counting operations

• assume these steps take constant time:
  • mathematical operations
  • comparisons
  • assignments
  • accessing objects in memory
  • function call and return
• then count the number of operations executed as function of size of input

import time
def c2f(c):
  return c*9/5 + 32  # 4 ops

def mysum(x):
  total = 0  # 1 op
  for i in range(x+1):  # loop x+1 times.  1 op for x+1
    total += i  # 2 ops
  return total  # 1 op

#mysum takes 2 + 3(x+1) ops

Counting operations is also inconsistent

• Goal: to evaluate different algorithms
• count depends on algorithm. Good
• count depends on implementation. Bad in some contexts, good in others
• count independent of computers. Good
• no clear definition of which operations to count. Bad
• count varies for different inputs and can come up with a relationship between inputs and time. Good!

Still need a better way

• timing and counting evaluate implementations.
• timing evaluates machines.

• want to evaluate algorithm
• want to evaluate scalability
• want to evaluate in terms of input size

Ideas

• Going to focus on idea of counting operations in an algorithm, but not worry about small variations in implementation (e.g., whether we take 3 or 4 primitive operations to execute the steps of a loop)
• Going to focus on how algorithm performs when size of problem gets arbitarily large
• Want to relate time needed to complete a computation, measured this way, against the size of the input to the problem
• Need to decide what to measure, given that actual number of steps may depend on specifics of trial

Need to choose which input to use to evaluate a function

• want to express efficiency in terms of size of input, so need to decide what your input is
• could be an integer, e.g., mysum(x).
• could be length of a list, e.g., listSum(ls).
• you decide when multiple parameters to a function, e.g., searchForElement(ls, e).

Different inputs change how the program runs

• a function that searches for an element in a list

  def searchForElement(ls, e):
    for i in ls:
      if i == e:
        return True
    return False
  

• when e is first element in the list: BEST CASE
• when e is not in the list: WORST CASE
• when look through about half of the elements in the list: AVERAGE CASE
• want to measure this behaviour in a general way

BEST, AVERAGE, WORST cases

• suppose you are given a list L of some length len(L).
• best case: minimum running time over all possible inputs of a given size, len(L):
  • constant for searchForElement
  • first element in any list
• average case: average running time over all possible inputs of a given size, len(L)
  • May use a practical measure to define frequency of each possible input
• worst case: maximum running time over all possible inputs of a given size, len(L)
  • linear in length of list for searchForElement
  • must search entire list and not find it
  • We will generally focus on this case

Orders of growth. Goals:

• Want to evaluate program's efficiency when input is very big
• Want to express the growth of program's run time as input size grows
• Want to put an upper bound on growth --- as tight as possible
• Do not need to be precise: "order of", not "exact" growth
• We will look at largest factors in run time (which section of the program will take the longest to run?)
• Thus, generally, we want tight upper bound on growth, as function of size of input, in worst case

Measuring Order of Growth: Big Oh Notation

• Big Oh notation measures an upper bound on the asymptotic growth, often called order of growth
• Big Oh or O() is used to describe worst case
  • worst case occurs often and is the bottleneck when a program runs
  • express rate of growth of program relative to the input size
  • evaluate algorithm NOT machine or implementation

Exact steps vs. O():

def fact_iter(n):
  """ assumes n an int >= 0 """
  answer = 1
  while n > 1:  # comparison is 1 step
    answer *= n #2 steps
    n -= 1  #2 steps
  return answer

• computes factorial
• number of steps: 1 + 5n + 1
• worst case asymptotic complexity: O(n)
  • ignore additive constants
  • ignore multiplicative constants

What does O(n) measure?

• Interested in describing how amount of time needed grows as size of (input to) problem grows
• Thus, given an expression for the number of operations needed to compute an algorithm, want to know asymptotic behaviour as size of problem gets large
• Hence, will focus on term that grows most rapidly in a sum of terms
• And will ignore multiplicative constants, since want to know how rapidly time required increases as we increase size of input

Simplification examples

• drop constants and multiplicative factors
• focus on dominant terms

O(n^2): n^2 + 2n + 2
O(n^2): n^2 + 10000000n + 3^10000
O(n): log(n) + n + 4
O(n log(n)): 0.0001*n*log(n) + 300n
O(3^n): 2n^30 + 3^n

Examples of Types of Order of Growth

Analyzing programs and their complexity

• combine complexity classes
  • analyze statements inside functions
  • apply some rules, focus on dominant term
• Law of addition for O():
  • used with sequential statements
  • O(f(n)) + O(g(n)) is O(f(n)+g(n))
  • For example:

    for i in range(n):  #O(n)
      print('a')
    for i in range(n*n):  #O(n^2)
      print('a')
    

    is O(n)+O(n^2) which is O(n+n^2) which is O(n^2) because of dominant term.

Analyzing programs and their complexity

• combine complexity classes
  • analyze statements inside functions
  • apply some rules, focus on dominant term
• Law of multiplication for O():
  • used with nested statements or loops.
  • O(f(n))*O(g(n)) is O(f(n)*g(n)).
  • for example:

    for i in range(n):  #n loops, each O(n), for a total of O(n)*O(n)
      for j in range(n):
        print(a)
    

    O(n)*O(n) is O(n*n) is O(n^2) because the outer loop goes n times and the inner loop goes n times for every outer loop iteration.

Complexity Classes

• O(1) denotes constant running time
• O(log n) denotes logarithmic running time
• O(n) denotes linear running time
• O(n log(n)) denotes log-linear running time
• O(n^c) denotes polynomial running time (c is a constant)
• O(c^n) denotes exponential running time (c is a constant raised to a power based on size of input)

Complexity classes ordered low to high

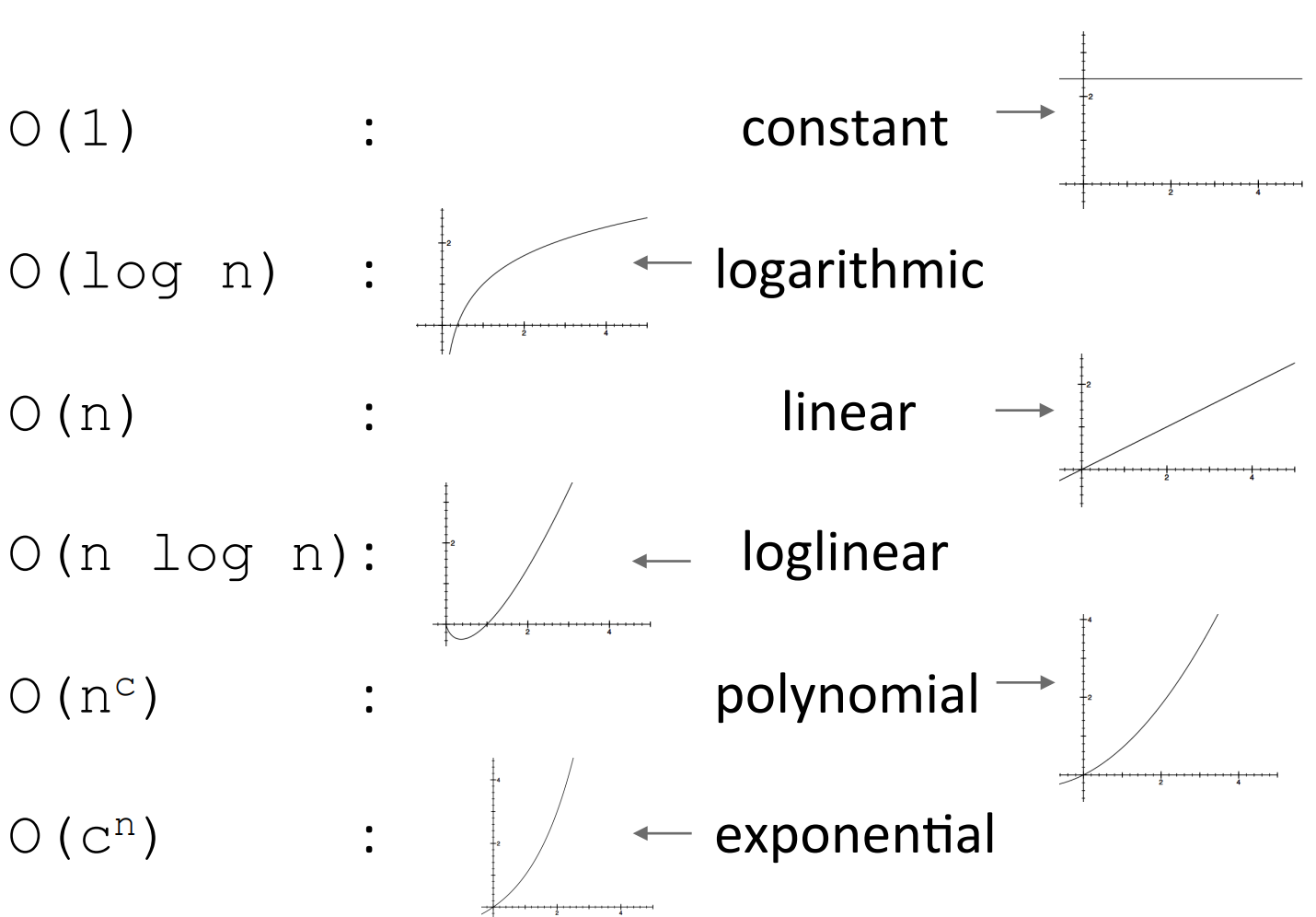
Complexity growth

Class	n=10	n=100	n=1000	n=1000000
O(1)	1	1	1	1
O(log n)	1	2	3	6
O(n)	10	100	1000	1000000
O(n log(n))	10	200	3000	6000000
O(n^2)	100	10000	1000000	1000000000000
O(2^n)	1024	1.2*10^31	1.07*10^311	forget it!

Linear complexity: Simple iterative loop algorithms are typically linear in complexity.

Linear search on unsorted list

def linearSearch(L, e):
  found = False
  for i in range(len(L)):
    if e == L[i]:
      found = True  # can speed up a little by returning True here
                    # but speed up doesn't impact worst case
  return found

• must look through all elements to decide it's not there
• O(len(L)) for the loop * O(1) to test if e == L[i]. Subtle: assumes we can retrieve element of list in constant time.
• O(1+4n+1) = O(4n+2) = O(n).
• overall complexity is O(n) where n is len(L).

Constant-time list access

Linear search on sorted list

def search(L, e):
  for i in range(len(L)):
    if L[i] == e:
      return True
    if L[i] > e:
      return False
  return False

• must only look until reach a number greater than e
• O(len(L)) for the loop * O(1) to test if e == L[i]. Worst case will need to look at whole list.
• overall complexity is O(n) where n is len(L)
• NOTE: order of growth is same, though run time may differ for the two search methods (sorted and unsorted)

Linear algorithm: add characters of a string, assumed to be composed of decimal digits

def addDigits(s):
  val = 0
  for c in s:
    val += int(c)
  return val

Linear complexity example: complexity often depends on the number of iterations

def fact_iter(n):
  prod = 1
  for i in range(1, n+1):
    prod *= i
  return prod

• number of times around loop is n
• number of operations inside loop is a constant (in this case, three; set i, multiply, set prod)
  • O(1+3n+1) is O(3n+2) is O(n)
• Overall just O(n)

Nested loops

• simple loops are linear in complexity
• what about loops that have loops within them?

Quadratic complexity: determine if one list is subset of second, i.e., every element of first, appears in second (assume no duplicates)

def isSubset(L1, L2):
  for e1 in L1:
    matched = False
    for e2 in L2:
      if e1 == e2:
        matched = True
        break
    if not matched:
      return False
  return True

• Outer loop executed len(L1) times
• Each iteration will execute inner loop up to len(L2) times, with constant number of operations: O(len(L1)*len(L2)).
• Worst case when L1 and L2 same length, all of elements of L1 in L2. The outer loop iterates O(len(L1)) times, and the inner loop iterates O(len(L2)/2) times on average (averaged over outer loop iterations). Given that the lists are of equal length, let n=len(L1)=len(L2), then the worst-case running time of this program is O(n^2).

Quadratic complexity example: Find intersection of two lists, return a list with each element appearing only once.

def intersect(L1, L2):
  tmp = []
  for e1 in L1:
    for e2 in L2:
      if e1 == e2:
        tmp.append(e1) #collect all intersections in tmp
        break
  res = []
  for e in tmp:
    if not(e in res):
      res.append(e)  #eliminate duplicates
  return res

• First nested loop takes len(L1)*len(L2) steps
• Second loop takes at most len(tmp) steps, which is at most len(L1).
• Determining e in res takes at most len(res) steps which can be at most min(len(L1),len(L2)).
• If we assume lists are of roughly same length, then the running time is O(len(L1)^2).